模拟电子技术基础-频率响应
基本要求
- 掌握放大电路频率响应的基本概念和描述方法
- 了解各元件参数对放大电路的频率响应性能的影响
- 了解放大电路不同组态频率响应的特点
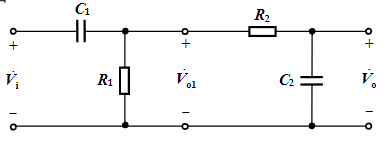
R1C1>>R2C2 and C1>>C2
R1C11<<ω<<R2C21
故等效为:
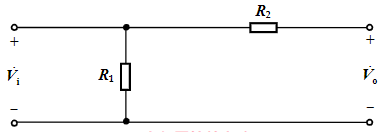
∣A˙vM∣=1,φ=0°
R1C11<<R2C21<<ω
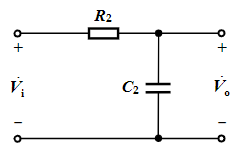
A˙vH=1+jωR2C21=1+j(f/fH)1 when fH=2πR2C21∣A˙vM∣=1+(f/fH)21, φ=−arctan(f/fH)
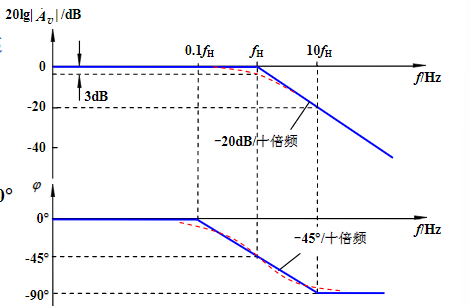
注:横坐标也是对数值。
ω<<R1C11<<R2C21
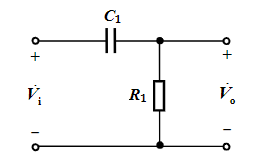
A˙vL=1+jωR2C2jωR2C2=1−j(fL/f)1 when fL=2πR1C11∣A˙vM∣=1+(fL/f)21, φ=arctan(fL/f)
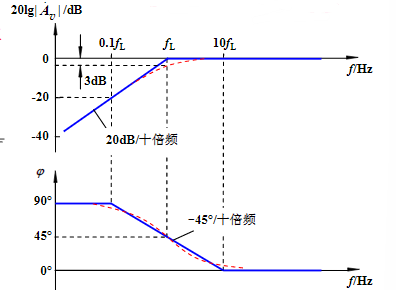
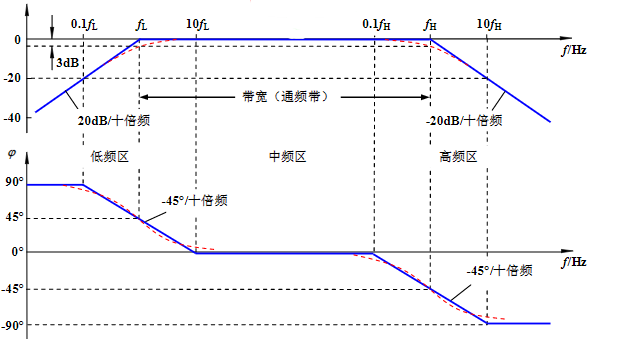
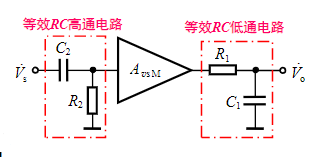
将放大电路抽象为以上模型,运用一阶RC频率响应的方法求解。
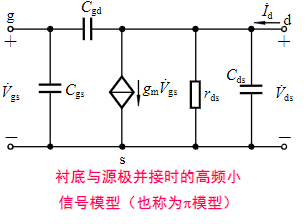
高频小信号,考虑极间电容。
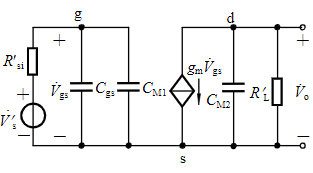
CM1=(1+gmRL′)Cgd, CM2可忽略Rsi′=RSi//RgRL′=Rd//RL∣AvsM⋅fH∣≈2πRsiCgd1
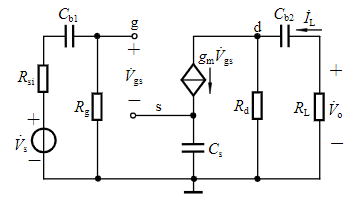
两个耦合电容,一个旁路电容,
fL1=2π(Rsi+Rg)Cb11fL2=2π(1/gm)Cs1fL3=2π(Rd+RL)Cb21