算法设计与分析复习

5332字约18分钟

2022-06-09

《算法设计与分析》课程的复习笔记。

后面复习不完了，🐒🐒🐒

算法是一组有穷的规则，它规定了解决某一特定类型问题的一系列运算。
循环不变式证明算法正确性：
初始化时循环不变式在循环开始之前为真
证明每次循环之后循环不变式仍然为真
循环可以有限次终止
算法的五个重要特性：
确定性
能行性
输入
输出

算法效率分析

算法时间复杂度限界函数：

上界 $\mathcal{O}$ 记号
$\mathcal{O}(g(n)) = \{f(n): \exist \ c ,n_0,s.t. 0\le f(n) \le cg(n)\,\ \forall\ n\ge n_0\}$
下界 $\mathcal{\Omega}$ 记号
$\mathcal{\Omega}(g(n)) = \{f(n): \exist \ c ,n_0,s.t. 0\le cg(n) \le f(n)\,\ \forall\ n\ge n_0\}$
渐进紧缺界 $\mathcal{\Theta}$ 记号

\mathcal{\Theta}(g(n)) = \{f(n): \exist \ c_1, c_2 ,n_0,s.t. 0\le c_1g(n) \le f(n) \le c_2g(n)\,\ \forall\ n\ge n_0\}

通过递推式计算算法复杂度

代换法

先猜测解的形式，然后用数学归纳法求解中的常数，并证明解是正确的。

递归树法

标上每层的代价和，以及特殊的叶子 🍃 层。一般假设 $T(1)=\mathcal{O}(1)$ ，叶子层代价则为叶子数。同样的通过递归树猜解，然后用数学归纳法证明。

🌟 主定理法

如果递归式具有如下形式，可以用主定理直接给出渐进界：

T(n)\ =\ aT(n/b)\ +\ f(n)

关注 $f(n)$ 与 $n^{\log_ba}<\text{递归树最底层代价=分支}^{\text{层数}}=a^{\log_bn}\ =n^{\log_ba}>$ 的阶数关系，取较大（需要大一个多项式因子）的那个作为 $T(n)$ ：

$\exist\ \epsilon\ \gt\ 0,\ f(n)\ =\ \mathcal{O}(n^{\log_b{a-\epsilon}}) \implies\ T(n)\ =\ \Theta(n^{\log_ba})$
$\exists\ \epsilon\ \gt\ 0,\ f(n)\ =\ \Omega(n^{\log_b{a-\epsilon}})\ \bigwedge\ \exists\ c\ \lt\ 1,\ af(n/b)\ \le\ cf(n)\ \implies\ T(n)\ =\ \Theta(f(n))$
$f(n)\ =\ \Theta(n^{\log_ba})\ \implies\ T(n)\ =\ \Theta(f(n)\log n)$

可以了解到主定理具有间隙，那么考虑方法 1 与方法 2.

分治法

当问题规模比较大而无法求解时，将原始问题分解为几个规模较小、但类似于原始问题的子问题，然后递归地求解这些问题，最后合并子问题的解以得到原始问题的解。

🌰 最大子数组

问题：求解和最大的连续子数组。

分：将数组划分为左边和右边

治：将左边和右边分别递归求解 $T(n/2)$

合：另外计算跨越中点的数组最大和（从中点往左统计，从中点往右统计， $\mathcal{O}(n)$ ），取左、右、中最大的值

递推式： $T(n) = 2*T(n/2)\ +\ n$

复杂度： $T(n)\ =\ \mathcal{O}(n\lg n)$

动态规划

动态规划原理

动态规划通过拆分问题，将问题拆分为许多的子问题，定义问题状态和状态之间的关系（即状态转移方程），使得问题能够以递推方式解决。包含以下三个特征：

最优子结构：问题的最优解包含子问题的最优解。
无后效性：推到后面阶段状态的时候只需关心前面阶段的值。
重复子问题：不同的决策序列，到达某个相同的阶段时，可能会产生重复的状态。

最优子结构的证明

剪切-粘贴法（反证法）证明：假设最优解中的子问题解不是子问题的最优解，那么将该解剪切，将子问题更优的解粘贴进去从而得到一个总体更优的解，这与最优解假设矛盾，故最优解中的子问题的解是子问题的最优解，证毕。

🌰 钢条切割

给定一段长度为 n 英寸的钢条和一个价格表 P，求切割钢条方案，使得销售收益 $r_n$ 最大。

对于一根长度为 n 的钢条最多有 n 种切法即 ${(n-1, 1),(n-2,2),...,(0,n)}$ ，那么求解该问题的时候则考虑左边的钢条作为子问题，销售额为 $r_{left}\ +\ P_{right}$ ，那么对于钢条最优解则有

r_n\ =\ \max_{i=1}^{n}\{r_{n-i}\ +\ P_i\}

即对应的状态转移方程，于是我们自底向上，即 n 从小到大一次算出 $r_n$ 并保存。

如果需要具体方案，那么我们可以保存对于长度为 n 的钢条，最优切点在何处，即新建 S 表，保存长度为 n 时，右边段大小为多少，就是当取到 max 时 i 的值。这样，我们可以通过递推的方式回去，依次找到所有的 i，即是钢条切割方案。

🌰 矩阵链乘法

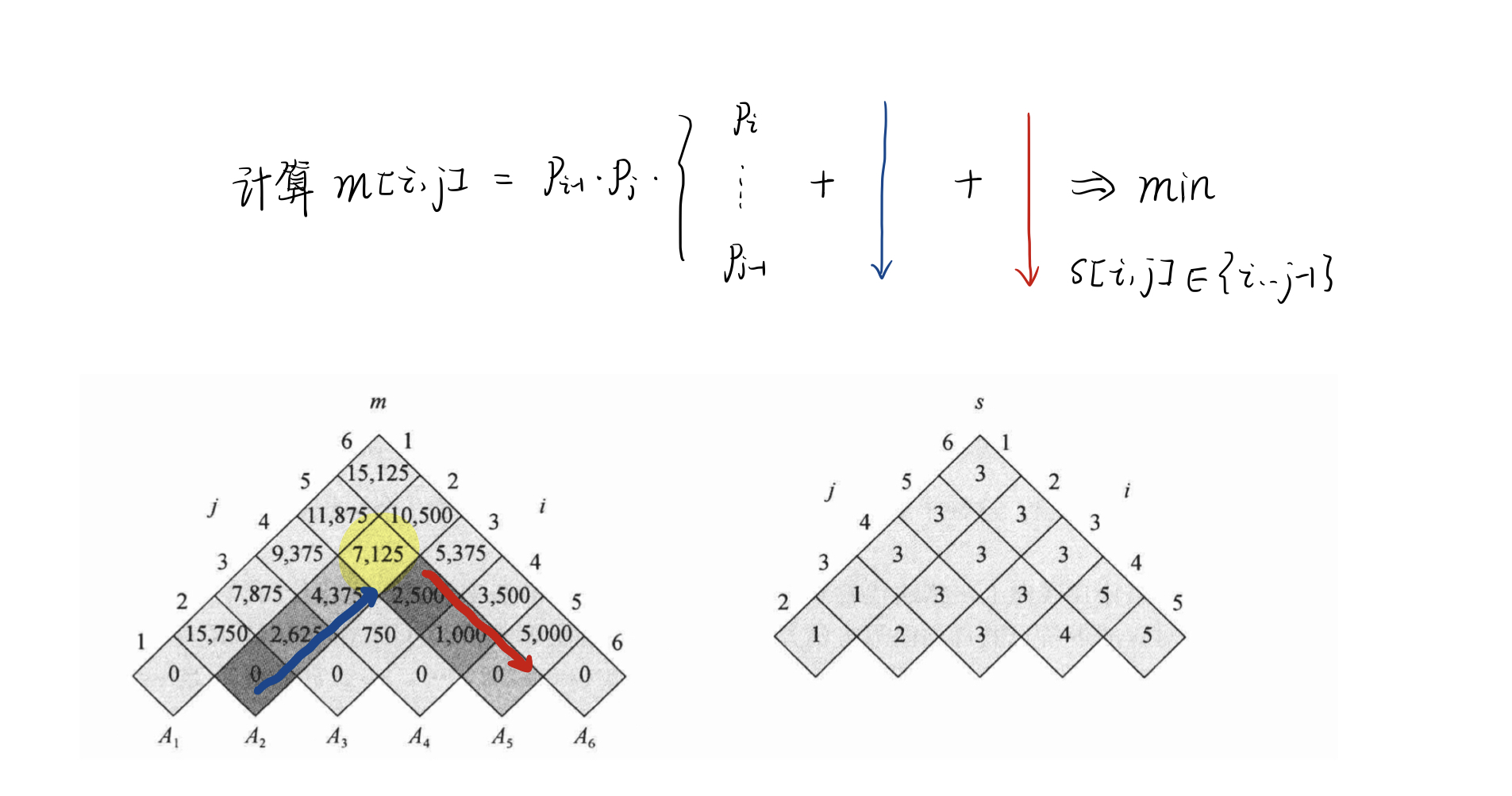
n 个要连续相乘的矩阵构成一个矩阵链 $<A_1,\ A_2,\ ...,\ A_n>$ ，要计算这 n 个矩阵的连乘乘积。不同的计算模式（先算哪部分）代价是不同的，需要找出最小代价方法。

同样的该问题具有最优子结构。那么假设 $m[i,\ j]$ 表示 $<A_i,\ ...,\ A_j>$ 子问题的最优解。则有递推式， $p_i,\ i=0\to n$ 表示矩阵链的规模大小。

用 $s[i,\ j]$ 表示使 $m[i,\ j]$ 最小值的 $k$ ，则可以依次构造。

🌰 最长公共子序列（Longest-Common-Subsequence, LCS）

给定两个序列 X 和 Y，若序列 Z 既是 X 的子序列也是 Y 的子序列，则称 X 是 X 和 Y 的公共子序列。需要求解最长的公共子序列。

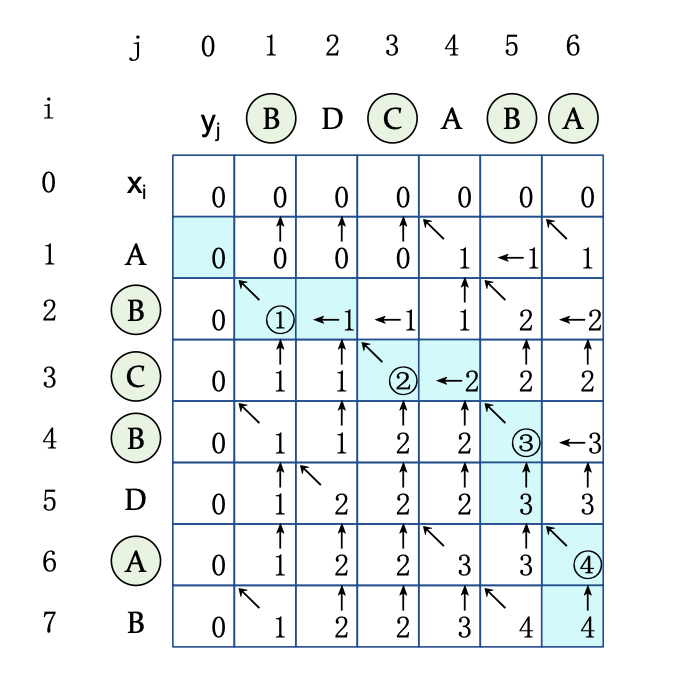
记 $c[i,\ j]$ 为前缀序列 $X_i$ 与 $Y_j$ 的一个 LCS 的长度，则有：

另外构造表 $b[i,\ j]$ 表示依赖前面的哪一项。在 dp 手算则与 c 表一起出现，变成了箭头表示。

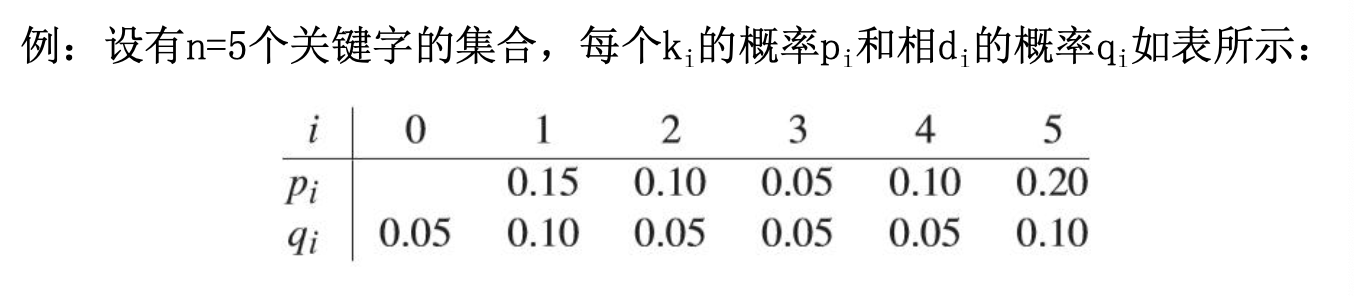
🌰 最优二叉搜索树

给定一个 n 个关键字的已排序的序列 $K\ =\ <k_1,\ k_2,\ ...\ ,\ k_n>$ ，对于每个关键字 $k_i$ ，都有一个概率 $p_i$ 表示其被搜索的频率，那么对于搜索失败的情景则有 $q_i$ 概率表示。

子序列的最优二叉树是作为序列最优二叉树的子树出现的，设 $w[i,\ j]=\sum_{l=i}^jp_l\ +\ \sum_{l=i-1}^jq_l$ 表示子树概率之和，设 $e[i,\ j]$ 表示第 $i$ 到第 $j$ 个关键字生成的最优二叉搜索树的代价，首先应当计算由子树代价推出合并后的代价：

计算思路：树变为子树，深度加一。以及加上新增的根节点作为新代价。

root=r\implies new[i,\ j]\ =\ (e[i,\ r-1]+w[i,r-1])\ +\ (e[r+1,j]+w[i+1,j])\ +\ p_r

因 $w[i,\ j]\ =\ w[i,\ r-1]\ +\ p_r\ +\ w[r+1,\ j]$

故 $new[i,\ j]\ =\ e[i,\ r-1]\ +\ e[r+1,\ j]\ +\ w[i,\ j]$

于是递推式为

需要三个表：

$e[1..n+1,\ 0..n]$ ：用于记录 $e[i,\ j]$ 的值

$root[1..n,\ 1..n]$ ：用于记录所有最优二叉搜索子树的根节点

$w[1..n+1,\ 0..n]$ ：用于保存子树节点概率之和，且有 $w[i,\ j]\ =\ w[i,\ j\ -\ 1]\ +\ p_j\ +\ q_j$

🌰 0-1 背包问题

给定重量和价格为 $(w_i,\ v_i)$ 的 n 个物品，在满足背包容量 $C$ 下，求包内总价值最大。0-1 指物品最多只能被放一次。

令 $F(i,\ j)$ 表示将前 $i$ 件物品放入容量为 $j$ 的背包中。那么有状态转移方程：

F(i,\ j)\ =\ \max(F(i-1,\ j),\ F(i-1,\ j-w[i])\ +\ v_i)

如果用二维数组，可以了解到结果只依赖于前一行的左上区域，那么可以从后往前算做一维空间优化，则有：

F(j)\ =\ \max(F(j),\ F(j-w[i]\ )+\ v_i)

贪心算法

贪心算法原理

贪心选择：可以通过做出局部最优选择来构造全局最优解性质
最优子结构：问题的最优解包含子问题的最优解
贪心正确性证明：思路是设结果集合没有贪心选择元素，即将集合中首选元素替换成贪心选择元素依然是最优解。

🌰 活动选择问题

假定有一个活动的集合 $S$ 包含有 $n$ 个活动 $\{a_1,\ a_2,...,\ a_n\}$ ，每个活动 $a_i$ 都有一个开始时间 $s_i$ 和结束时间 $f_i$ ， $0\le s_i\le f_i \lt \infty$ 。同时，这些活动都要使用同一资源，而这个资源在任何时刻只能供一个活动使用。活动选择问题：从集合中挑选最大兼容活动集合。

不失一般性，活动按结束时间非递减排序。

贪心：每次选择结束时间最早而且开始时间不早于上一挑选活动的结束时间的活动。

正确性同理：任意非空子问题 $S_k$ ，令 $a_m$ 是 $S_k$ 中结束时间最早的活动，则 $a_m$ 必然在 $S_k$ 的某个最大兼容活动子集中。

证明：设 $A_k$ 是 $S_k$ 的一个最大活动子集，且 $a_j$ 是 $A_k$ 中结束最早的活动。若 $a_j = a_m$ 则直接得证。若不是，令 $A_k'=(A_k-\{a_j\})\mathop{\cup}\{a_m\}$ .

因为 $A_k$ 中的活动都是不相交的， $a_j$ 是 $A_k$ 中结束时间最早的活动，而 $a_m$ 是 $S_k$ 中结束时间最早的活动，所以 $f_m\le f_j$ ，即 $A_k'$ 中的活动也是不相交的。

由于 $|A_k'|=|A_k|$ ，所以 $A_k'$ 也是 $S_k$ 的一个最大兼容活动子集，这个子集包含 $a_m$ 得证

🌰 哈夫曼编码问题

贪心：每次从中选出频率最低的两个节点进行合并，得到的新节点继续加入集合合并，这样就可以构造一棵编码树——哈夫曼树。

图搜索问题

基本图 $G\ =\ (V,\ E)$ ，常用数据结构邻接表、邻接矩阵。

广度优先搜索

从结点 $v$ 开始，首先访问结点 $v$ ，给 $v$ 标上已访问标记。
访问邻接 $v$ 且目前未被访问的所有结点，此时结点 $v$ 被检测，而 $v$ 的这些邻接结点是新的未被检测的结点。将这些结点依次放置到一个称为未检测结点表的队列中。
若未检测结点表为空，则算法终止；否则从队列中取出结点检测。

深度优先搜索

从结点 $v$ 开始，首先访问 $v$ ，标记已访问，然后访问邻接结点 $w$ ，开始新的检测。当 $w$ 检测完毕后再恢复对 $v$ 的检测。所有可达结点都被检测完毕后算法终止。

D_Search

改造 BFS 算法，未被检测结点用栈来保存。

回溯算法

回溯的非递归形式：

procedure back-track:
  while not terminated:
		if 被回退到了非法层: terminated = true
		if 本层中未考虑元素数量为 0: 撤销本层操作，回退上一层
		考察本层中未被考察的元素
		如果在最底层，则添加结果
		进入下一层考察

回溯的递归形式：

procedure back-track(k):
	if 最底层: 存放结果，返回
	for 元素 in 本层元素:
		考察元素
		back-track(k + 1)
		撤销本次元素操作

分支限界算法

采取广度优先方法，对不满足限界要求的结点进行杀死。

L-C 检索（A* 算法）

采取代价估计函数，首选代价最小进行考察。

单源最短路问题

维护变量：

估计下界： $u.d$
满足估计下界的上一个结点： $u.\pi$

松弛操作：通过一条边对到一个点的距离上界进行更新。

上界性质： $u.d \ge \delta(s,u)$

三角形不等式： $\delta(s,u) \le \delta(s,v)+w(v,u)$

非路径（不存在路径）性质： $\delta(s,u)= \infty$

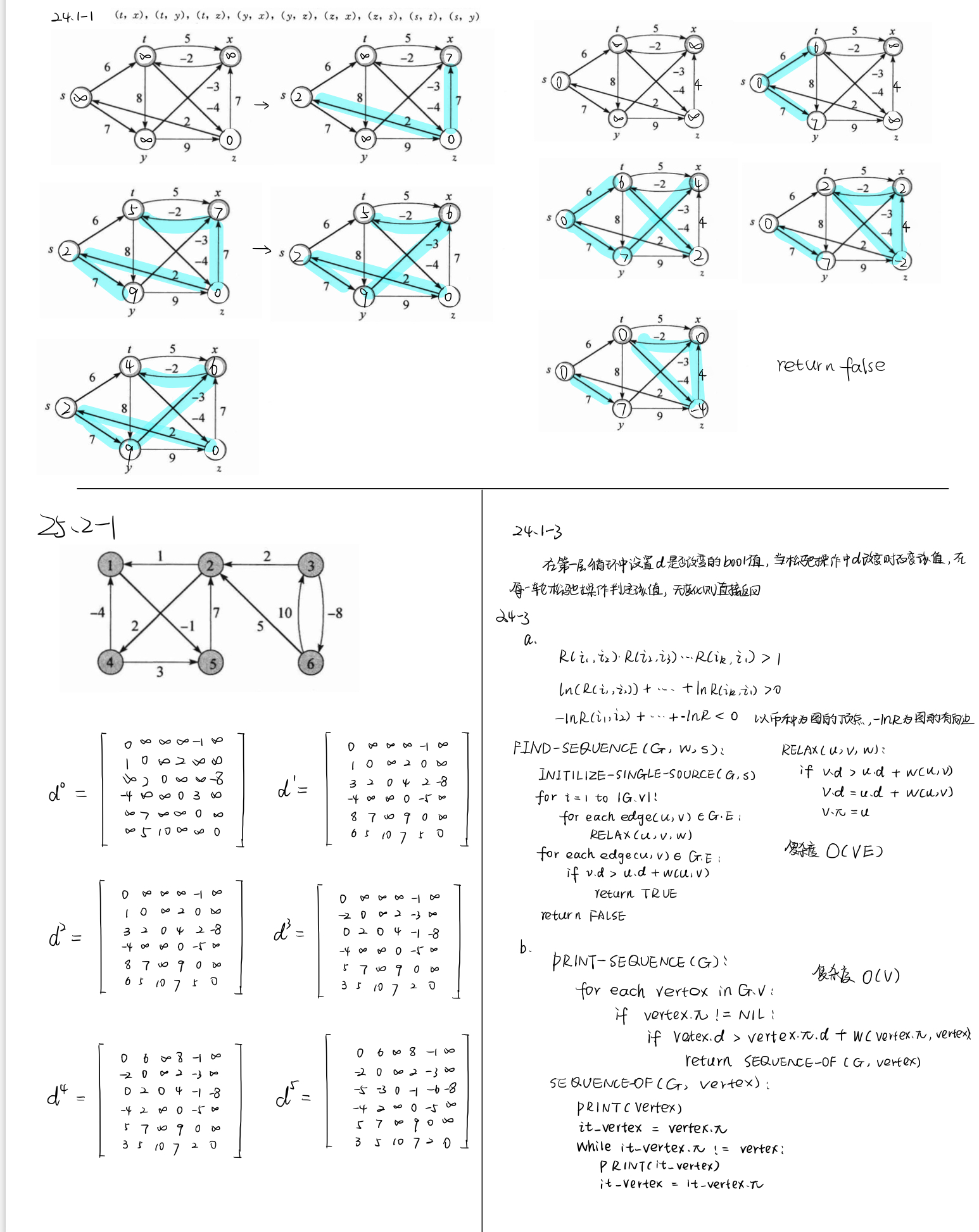
Bellmen-Ford 算法

BELLMAN-FORD(G, w, s)
	INITIALIZE-SINGLE-SOURCE(G, s)
	for i = 1 to |G.V| - 1:
		for each edge(u, v) \in G.E
			RELAX(u, v, w)
	for each edge(u, v) \in G.E
		if v.d > u.d + w(u, v)
			return FALSE
	return TRUE
	
INITIALIZE-SINGLE-SOURCE(G, s)
	for each vertex v \in G.V
		v.d = \infty
		v.\pi = NIL
	s.d = 0
	
RELAX(u, v, w)
	if v.d > u.d + w(u, v)
		v.d = u.d + w(u, v)
		v.\pi = u

对所有边松弛 $N-1$ 次，再遍历一遍边观察松弛情况，若还能松弛说明出现了负环。

Dijkstra 算法

Dijkstra 不能处理负权值边的图。Dijkstra 算法是一个贪心算法：每次总选择 V-S 集合中最短路径估计值最小的结点加入 S 中。

DIJLSTRA(G, w, s)
	INITIALIZE-SINGLE-SOURE(G, s)
	S = \emptyset
	Q = G.V
	while Q not equal \emptyset
		u = EXTRACT-MIN(Q)
		S = S \cup {u}
		for each vertex v \in G.Adj[u]
			RELAX(u, v, w)

算法复杂度分析：

朴素： $\mathcal{O}(V^2+E)$
二叉堆优化： $\mathcal{O}((V+E)\lg V)$
斐波那契堆优化： $\mathcal{O}(V\lg V + E)$

差分约束系统

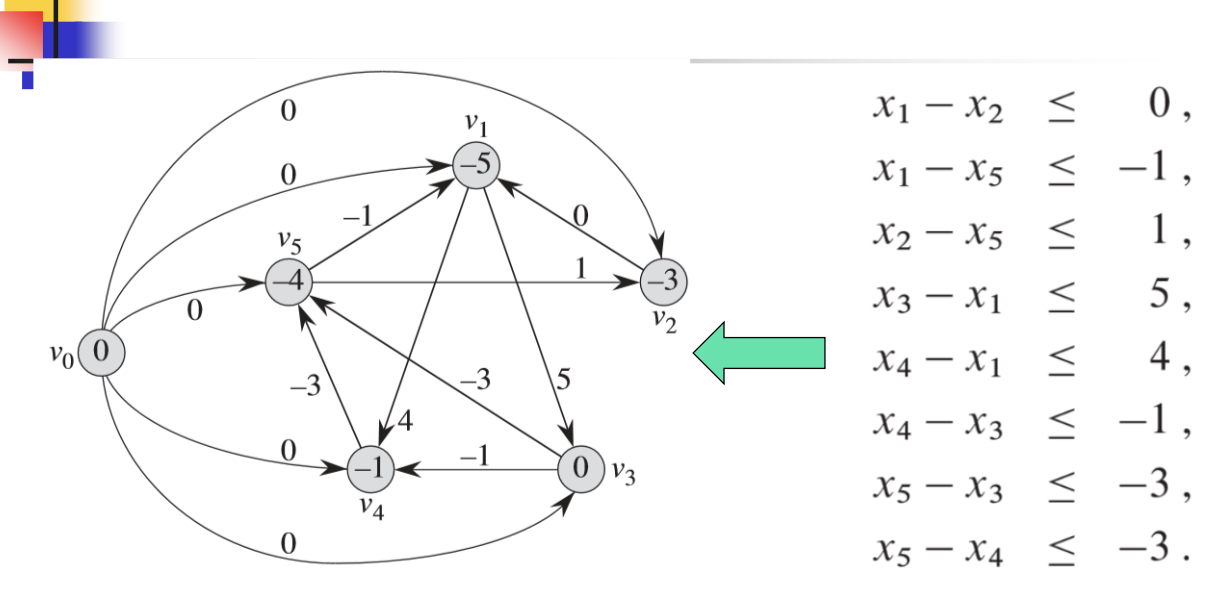
负权环则无解
否则解为最短路径及其偏移

所有结点对的最短路径问题

朴素的方法：每次迭代都对中间结点从 $1\to n$ 进行松弛检查。每次迭代需要 $\mathcal{O}(n^3)$ 操作，总共需要迭代 $n$ 次，故复杂度为 $\mathcal{O}(n^4)$ ，如果采用类似快速幂运算的方法能够减到 $\mathcal{O}(n^3\lg n)$ 复杂度。

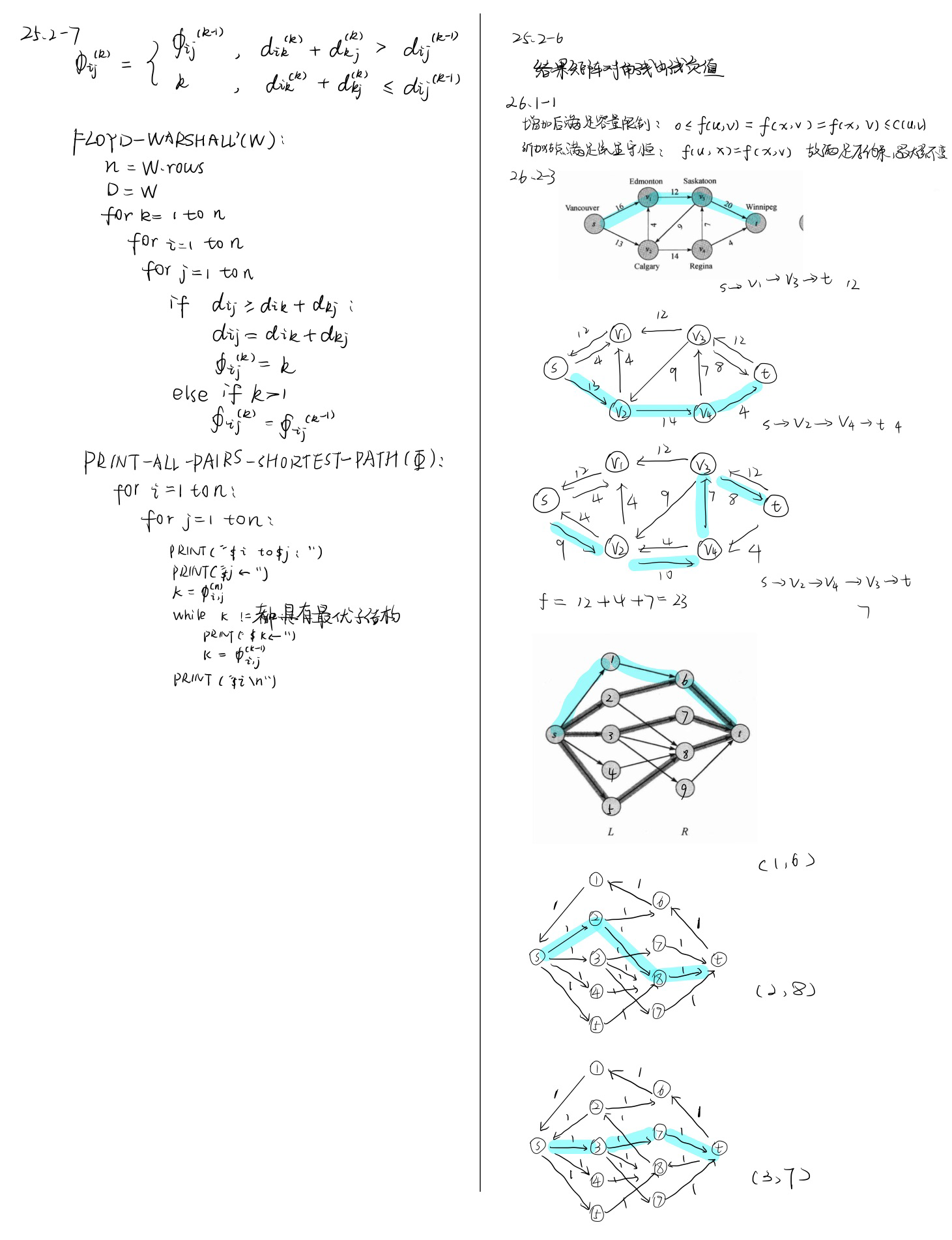
Floyd-Warshall 算法

对中间结点最大为 $k$ 进行迭代更新。需要 $\mathcal{O}(n^3)$ 复杂度。

Johnson 算法

先用一次 Bellmen-Ford 算法计算有无负权环路以及单源的距离下界。

再通过 $\hat{w}(u,v) =w(u, v)\ + \delta(s,u)\ -\ \delta(s,v)$ 变换权值使得所有边权值非负。

然后应用 n 次 Dijkstra 算法计算所有结点对。

这个算法依赖于 Dijkstra 算法实现。对于稀疏图首选这种方法。

最大流

Ford-Fulkerson 算法

选增广路径，更新。

最大二分分配

增加超级源结点和目标结点运用最大流算法。

作业复习

chp 1-2

对于插入排序需要运行 $8n^2$ 次，归并排序需要 $64n\lg n$ 次运算。 $n$ 的规模为多少时，插入排序性能优于归并排序？

8n^2<64n\lg n \implies 1\le n\le 43

$n$ 最小为多少时， $100n^2$ 规模算法优于 $2^n$ 规模算法？

100n^2 \le 2^n \implies n_{min} = 15

选择排序中的循环不变式是什么？为什么选择排序只要 $n-1$ 次迭代？最好情况和最坏情况下复杂度为多少？

循环不变式是 ”前 $i-1$ 个元素是最小的有序的 $i-1$ 个数“；

对于前 $n-1$ 个元素迭代后是最小的 $n-1$ 个数，那么最后一个数是最大的数，数组有序；

最好情况与最差情况都是 $\mathcal{O}(n^2)$

Chp 3

证明：
$f(n)=\Theta(g(n)) \Longleftrightarrow f(n) = \mathcal{O}(g(n))\ \bigwedge\ f(n)=\Omega(g(n))$

按照定义证明即可。

Chp 4

2-4（逆序对）
a. 插入排序的运行时间与输入数组中逆序对的数量之间是什么关系
b. 给出一个确定在 n 个元素的任何排列中逆序对数量的算法，最坏情况需要 $\Theta(n\lg n)$ 时间。

a. 正比关系。当将 $A[i]$ 插入至 $A[1..i-1]$ 中时，凡 $A[i]$ 作为逆序对后者构成逆序对的数都要移动，那么元素移动次数为 $A[2],A[3],...,A[n]$ 作为逆序对后者的个数之和，这个和就是逆序对的总数量。

b. 思路是修改归并排序中<并>这部分。

COUNT-INVERSIONS(A, p, r)
    if p < r
        q = floor((p + r) / 2)
        left = COUNT-INVERSIONS(A, p, q)
        right = COUNT-INVERSIONS(A, q + 1, r)
        inversions = MERGE-INVERSIONS(A, p, q, r) + left + right
        return inversions

MERGE-INVERSIONS(A, p, q, r)
    n1 = q - p + 1
    n2 = r - q
    let L[1..n1 + 1] and R[1..n2 + 1] be new arrays
    for i = 1 to n1
        L[i] = A[p + i - 1]
    for j = 1 to n2
        R[j] = A[q + j]
    L[n1 + 1] = ∞
    R[n2 + 1] = ∞
    i = 1
    j = 1
    inversions = 0
    for k = p to r
        if L[i] <= R[j]
            A[k] = L[i]
            i = i + 1
        else
        		// 将左边元素与右边元素合并时，这个元素与左边剩余比它大的元素构成逆序对
            inversions = inversions + n1 - i + 1
            A[k] = R[j]
            j = j + 1
    return inversions

4.1-5 阅读最大子数组和的滑动窗口解，写出理解

ITERATIVE-FIND-MAXIMUM-SUBARRAY(A)
    n = A.length
    max-sum = -∞
    sum = -∞
    for j = 1 to n
        currentHigh = j
        if sum > 0
            sum = sum + A[j]
        else
            currentLow = j
            sum = A[j]
        if sum > max-sum
            max-sum = sum
            low = currentLow
            high = currentHigh
    return (low, high, max-sum)

如果迭代前的子数组和小于 0，那么这段子数组对最大子数组没有贡献，故重新开始计算子数组和计算。从这些挑选出来的子数组中动态求最大的就是题解。

证明:
递归式 $T(n)=T(\lceil n/2 \rceil)\ +\ 1$ 的解是 $\mathcal{O}(\lg n)$

证明：

设 $T(n) = c\lg (n-2)$

求解： $T(n)=3T(\sqrt{n})+\log n$

解：令 $n=10^x$ ，那么有 $T(x)=3T(x/2)+x$

根据主定理的 $f(x)=x=\mathcal{O}(x^{\log_23-\epsilon})$ 其中 $\epsilon \approx 0.5$ ，故 $T(x)=\Theta(x^{log_2^3})$

那么 $T(n)=T(x(n))=\Theta((\log n)^{log_23})$

用递归树法证明 $T(n)=T(n/3)+T(2n/3)+cn$ 的解是 $\Omega(n\log n)$

解：画出递归树，可知每层（完整层）代价为 $cn$ ，将最浅层代价以下的枝减去，共有 $\lfloor \log_3^n \rfloor$ 层，即有 $T(n)\ge cn\lg n$

用主方法给出下列递归式的紧确渐进界，
a. $T(n)=2T(n/4)+n^{1/2}$
b. $T(n)=2T(n/4)+n^2$

a. $a=2,\ b=4,\ f(n)=n^{1/2},\ g(n)=n^{log_ba}=n^{log_42}=n^{1/2}$ ，由于 $f(n)=\Theta(g(n))$ ，符合主定理的第二种情况，故有 $T(n)=n^{1/2}\lg n$ .

b. $a=2,\ b=4,\ f(n)=n^2,\ g(n)=n^{log_ba}=n^{1/2}$ ，由于 $f(n)=\Omega(n^{1/2+\epsilon})$ ，其中 $\epsilon = 1.5$ ，符合主定理的第三种情况，故有 $T(n)=n^2$ .

主方法能否应用于递归式 $T(n)=4T(n/2)+n^2\log n$ ，为什么？给出此递归式的渐进上界。

$f(n) = n^2\log n,\ g(n)=n^2$ ，故位于主方法第二种情况与第三种情况的间隙，无法用主方法求解。

采用递归树：

每层代价 $n^2\log (n/2^i)$ ，共有 $\log_2^n$ 层，叶子代价为 $n^2$ .

故代价 $T(n)=n^2\log n\log_2n - \log2(1+2+...+log_2n)+\Theta(n^2)\le n^2\log n\log_2n+\Theta(n^2)$

故 $T(n)=\mathcal{O}(n^2\log^2n)$

动态规划

手算 dp 之矩阵链乘。

手算 dp 之 LCS。

手算 dp 之最优搜索二叉树。

利用 $w[i,\ j]\ =\ w[i,\ j\ -\ 1]\ +\ p_j\ +\ q_j$ 计算 $w$ 表。

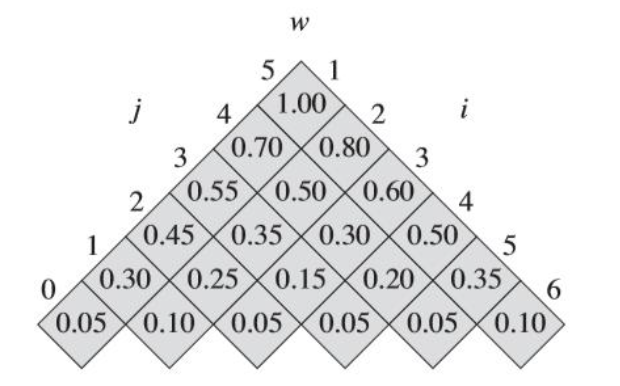
计算 $e$ 表和 $root$ 表。

假设钢条切割成本为 $c$ ，改造动态规划算法。

MODIFIED-CUT-ROD(p, n, c)
    let r[0..n] be a new array
    r[0] = 0
    for j = 1 to n
        q = p[j]
        for i = 1 to j - 1
            q = max(q, p[i] + r[j - i] - c)
        r[j] = q
    return r[n]

（字符串拆分）对于一个长度为 $n$ 的字符串进行一次拆分，需要 $\mathcal{O}(n)$ 的复杂度。
给定字符串 $s$ 以及拆分点数组 $L[1..m]$ ，求解字符串的拆分次序。

解：

$cost[0..m][1..m+1]$ ，令 $cost[i][j]$ 表示第 $i$ 个切分点到第 $j$ 个切分点的最小代价。

拓展 $L[0] = 0,\ L[m+1]=s.length$ .

$points[0..m][1..m+1]$ ，采用 $points[i][j]$ 保存第 $i$ 个切分点到第 $j$ 个切分点的第一个切点。

CUT-STRING(s, L):
	let cost[0..m][0..m+1] and points[0..m][1..m+1] be new tables
	L[0] = 0, L[m + 1] = s.length
	for i = 0 to m:
		for j = 1 to m + 1:
			cost[i][j] = \infity
	for i = 0 to m:
		cost[i][i + 1] = 0
  for l = 2 to m + 1:
  	for i = 0 to m + 1 - l:
  		j = i + l
  		for k = i + 1 to i + l - 1:
  			if cost[i][j] > L[j] - L[i] + cost[i][k] + cost[k][j]:
  				cost[i][j] = L[j] - L[i] + cost[i][k] + cost[k][j]
  				points[i][j] = k
  PRINT-ANS(points, 0, m + 1)

PRINT-ANS(points, i, j):
	if (i + 1 < j):
		return
	PRINT-ANS(points, i, points[i][j])
  print(" " + points[i][j] + " ")
  PRINT-ANS(points, points[i][j], j)

（库存规划）设 $d_i$ 为第 $i$ 个月的需求，一个月库存成本为 $h[j]$ ，多于 $m$ 台设备每个月需多付 $c$ 美元每台。求库存规划算法。

让 $cost[i][j]$ 表示前 $i$ 个月总共生产 $j$ 件商品的最小代价。

当 $x<0$ 时 $h(x),\ c(x)=0$

约束：当月有效状态需满足当月需求，即有效的 $j$ 取值为 $j(i) \ge D_i$

那么初始条件：

cost[1][j]= h(j-D_1)+c(j-m)

约束状态转移方程：

cost[i][j]=min_{0\le k\le j-D_{i-1}}{}\{cost[i-1][j-k]+h(j-D_i)+c(k-m)\}

15.3-6

贪心算法

（最小教室）求最小教室数量使得 $n$ 个活动相容。

按照结束时间非递减排序，每次挑选结束时间最早且活动开始时间不早于上一活动结束时间的活动，作为一个教室的集合。重复若干次，最终被划分成几个集合便是最小教室数量。

（指数乘积）贪心：一致策略排序

证明：

\exists\ i<j,\ s.t.\ a_i<a_j\wedge\ b_i>b_j\\ \frac{a_i^{b_j}a_j^{b_i}}{a_i^{b_i}a_j^{b_j}}=(\frac{a_j}{a_i})^{b_i-b_j}>1

找零问题

（分数背包问题）可以只拿一部分。

贪心，优先选单位最贵的。