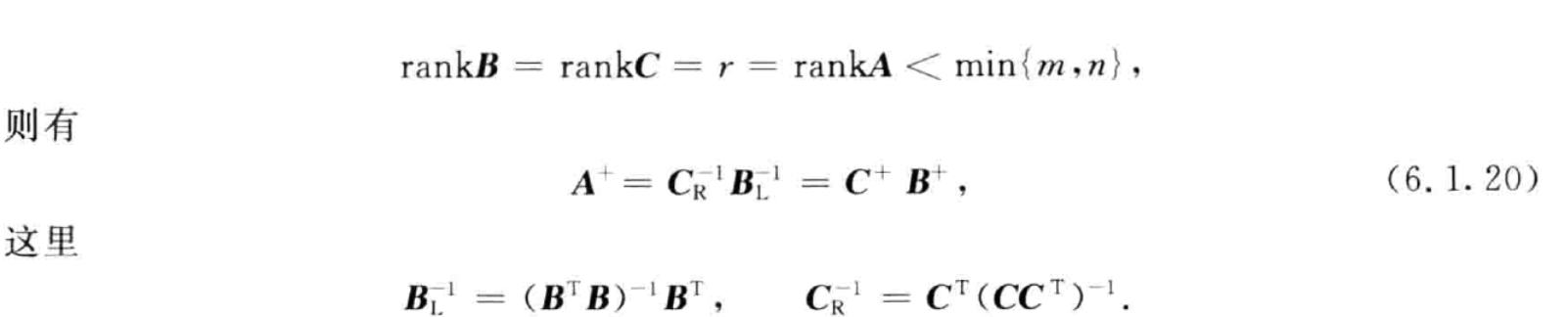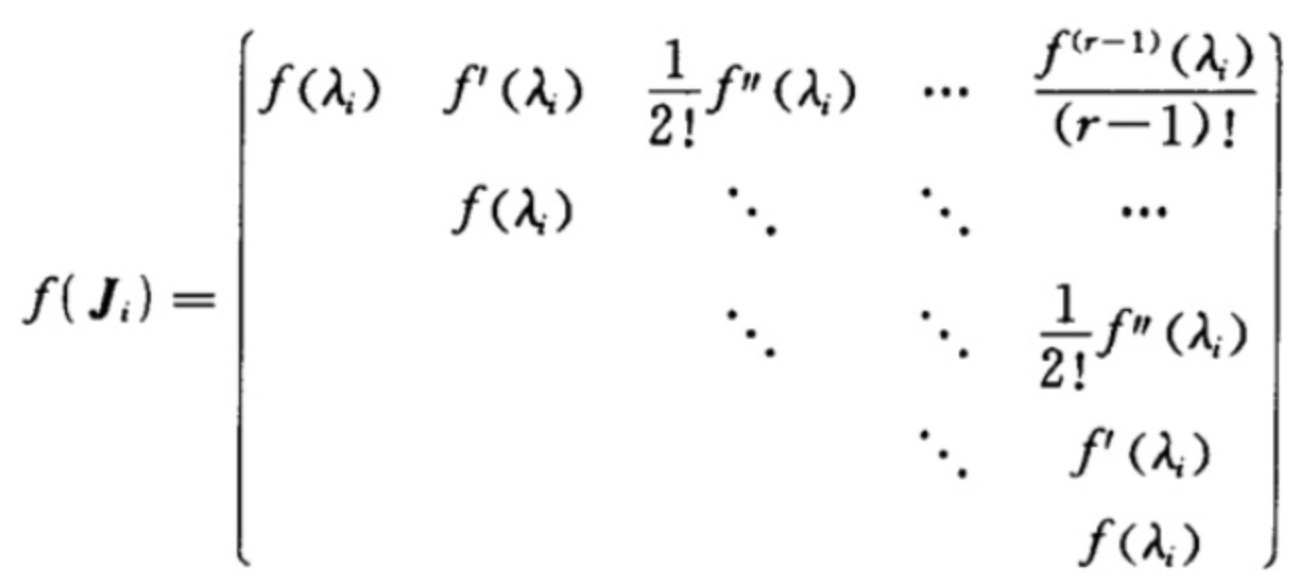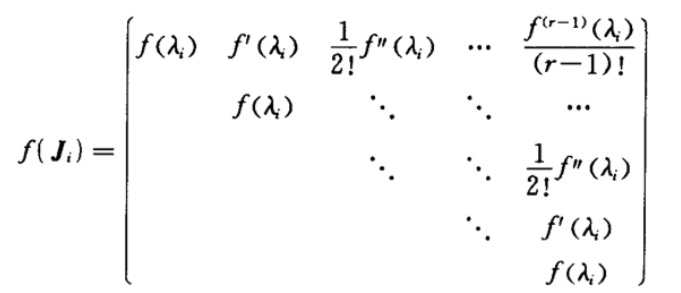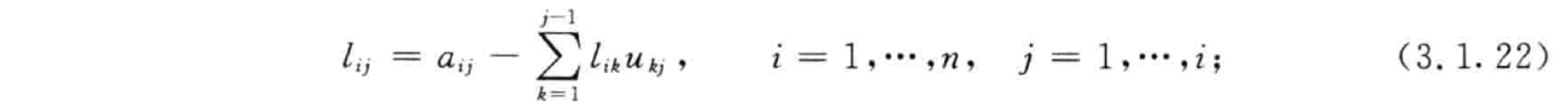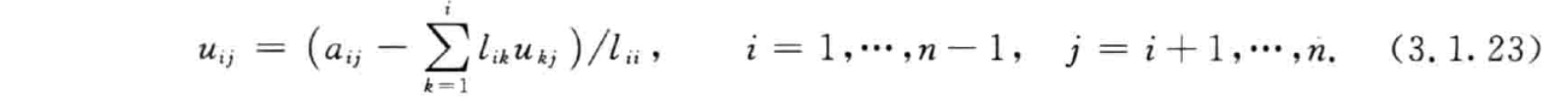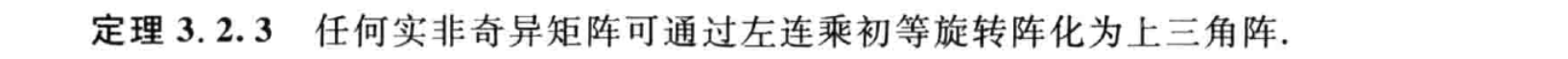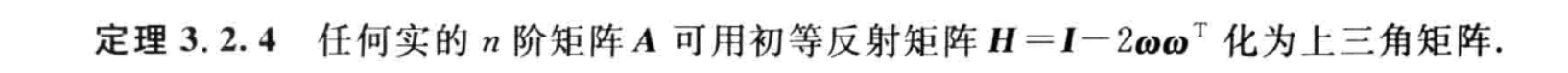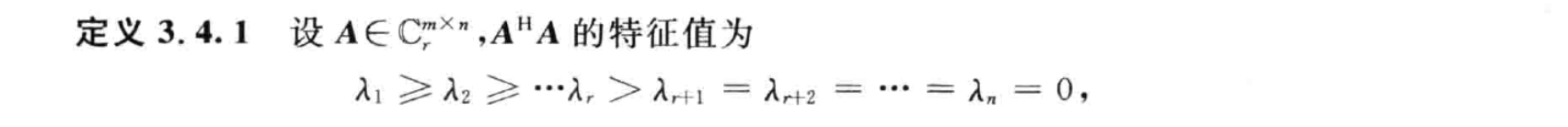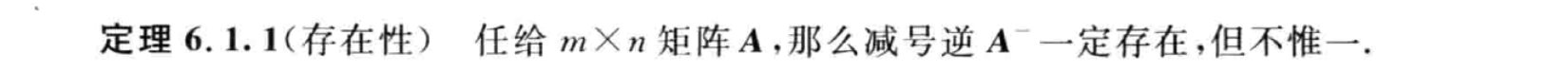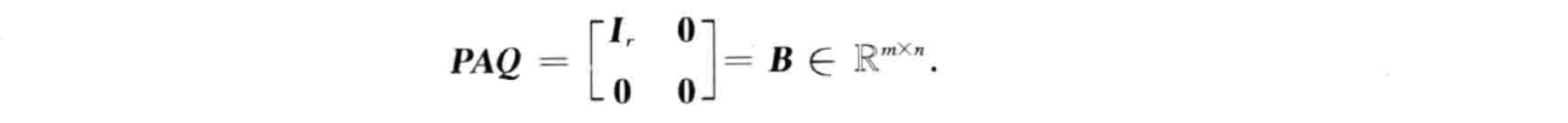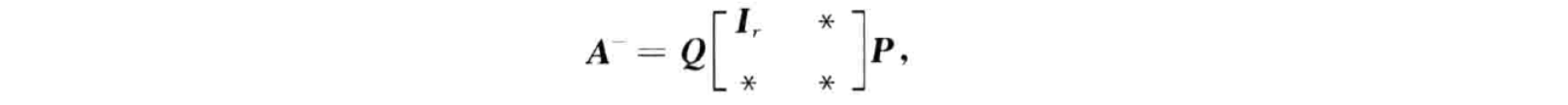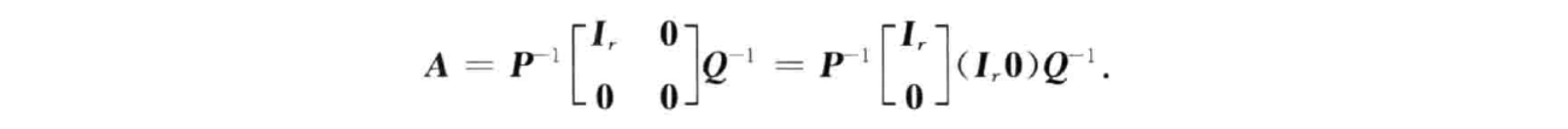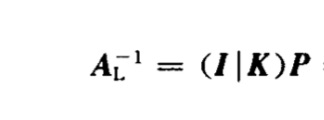研究生课程《矩阵论》课程笔记。包括线性空间与线性变换、Jordan标准形、矩阵的广义逆、矩阵分解等内容。
芳费
- 基变换与坐标变换
- 线性变换
{α1,α2,...,αn}, {β1,β2,...,βn} 是空间的两组基;
若有 βi=(α1,α2,...,αn)Ci ,即 (β1,β2,...,βn)=(α1,α2,...,αn)C
则称 C 为基 α→β 的过渡矩阵;
若 α=(α1,α2,...,αn)X,α=(β1,β2,...,βn)Y,
则 X=CY,Y=C−1X
线性变换的矩阵 A 的求法:
- 确定基
- 对基进行变换 T(αi)=∑kijαi
- 取 A=(kij)n×n
- 求解 Jordan 标准形
- Jordan 标准形的应用:高次幂等矩阵函数,求解微分方程
- 化零多项式应用:化简多项式,求矩阵逆,最小多项式(次数最低首一多项式)
J=J10⋮00J2⋮0⋯⋯⋱⋯00⋮Jk 其中 Ji=λi00⋮01λi0⋮001λi⋮0⋯⋯⋯⋱⋯000⋮λi
令矩阵 P 使得 AP=PJ
求法:
- ∣λI−A∣ 得 f(λ)=0 求特征值
- f(λ)=(λ−λ1)k1(λ−λ2)k2...(λ−λn)kn 其中 k 为代数重数
- 通过解 (λiI−A)X=0 求得 λi 对应的特征向量,特征向量的个数为几何重数。有几个特征向量则有几个 Jordan 块
- 若几何重数 < 代数重数,则求广义特征向量:(A−λi)X=x0 的解,其中 x0 为选取的特征向量。
- 特征向量,广义特征向量组成 P,特征值组成 J
f(A)=P(f(J))P−1
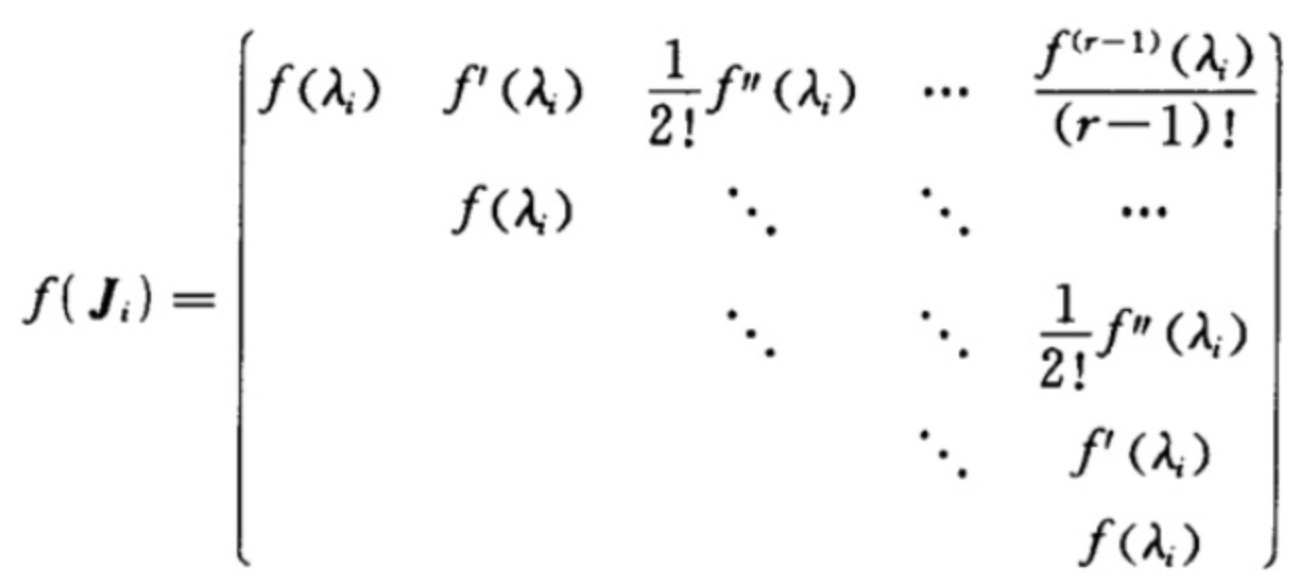
一阶线性非齐次微分方程 dxdy+P(x)y=Q(x) 的通解:
y=ce−∫P(x)dx+e−∫P(x)dx∫Q(x)e∫P(x)dxdx

f(λ)=0 则 f(A)=0
- 化简多项式 F(A)=F(A)modf(A)
- f(A)=0 通过移项可得 A−1
- 最小多项式:最小次的首一化零多项式,形式为 f(λ)=(λ−λ1)k1(λ−λ2)k2...(λ−λn)kn 其中 ki 表示特征值 λi 对应的 Jordan 块最大阶数
- 方阵的三角分解:LU、LDV 分解
- 矩阵的满秩分解 A=BC
- 可对角化矩阵的谱分解
- 可逆矩阵的 UR 分解
- 列满秩矩阵的 QR 分解
- Schur 分解
- 正规矩阵的性质
- 矩阵的奇异值分解
- 矩阵的极分解
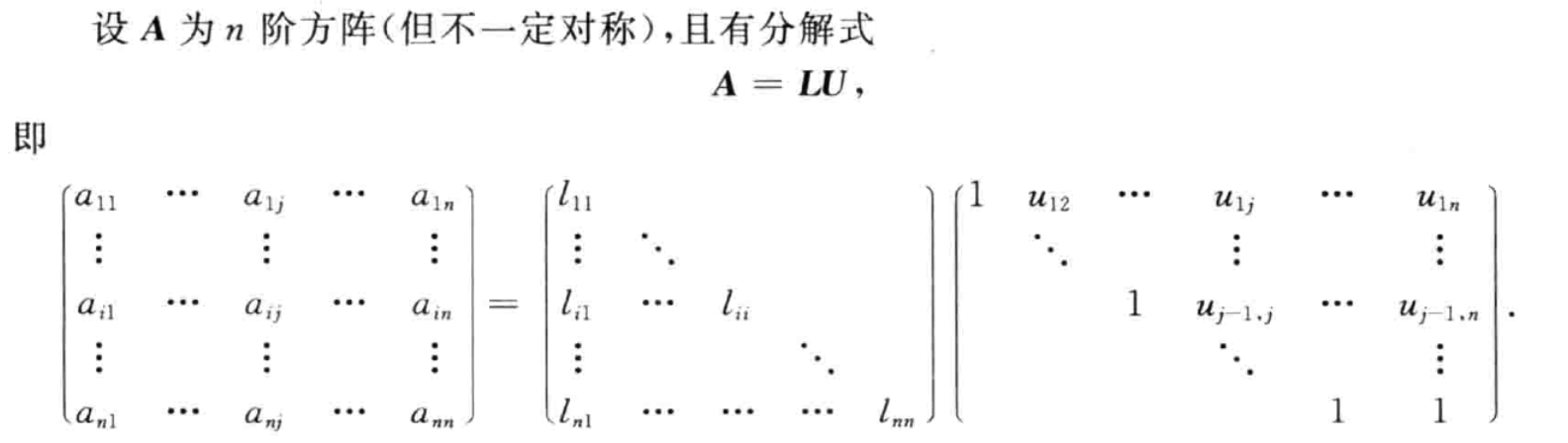
形式:A=LU。L,U分别为下三角矩阵、上三角矩阵
存在性:若 A 可以使用除行互换以外的初等行变换为上三角矩阵,则存在 LU 分解;若 A 的前 r 阶顺主子式不为 0,则存在 LU 分解
求法:解 A=LU 方程可得,固定 L 为单位下三角矩阵(Doolittle)。
应用:求解方程组 AX=b
- AX=LUX=b
- 令 Y=UX,则有 LY=b
- 利用回代法 LY=b 很好求出 Y
- 利用回代法 Y=UX 很好求出 X
形式:A=LDV。L,D,V 分别为单位下三角矩阵、对角矩阵、单位上三角矩阵
存在性:A=LDV 惟一的充要条件为 A 的所有顺主子式不为 0
求法:求出 LU 分解的 Doolittle 形式,将 U 中对角线元素按行除提取出一个对角矩阵 D
形式:A∈Cm×n,r(A)=r(B)=r(C)=r 使得 A=Bm×rCr×n
求法(初等行变换化成简化阶梯型):
例如 100200010340 ,非零行的第一个非零元为 1,其所在的列其他元素都为 0,即这些列是标准列 e
这里选取原矩阵 A 第 1,3 列做为 (A1 A3) 作为矩阵 B,阶梯型的前两行作为矩阵 C
应用:后章节求矩阵广义逆
形式:A=∑λiPi
存在性:可对角化矩阵
求法:
- 求出 A 的特征值 λi 以及对应的特征向量 αi
- A=∑λi(∣αi∣1⋅αiαiH)
形式:A=UR ,
// TODO!
形式:A=QR,Q 为正交矩阵,R 为上三角矩阵
求法:
Schmidt 正交化方法
⎩⎨⎧β1β2βn===α1,ϵ1=∣β1∣β1,α2−(ϵ1,α1)ϵ1,ϵ2=∣β2∣β2,......αn−∑i=1n−1(ϵi,αi)ϵi,ϵn=∣βn∣βn
Q=(ϵ1ϵ2...ϵn)
R=∣β1∣0(ϵ1,α2)∣β2∣⋯⋯⋱(ϵ1,αn)(ϵ2,αn)⋮∣βn∣
形式:AHA=AAH
常见的正规矩阵:
- 对角矩阵
- 实对称矩阵和反对称矩阵
- Hermite 矩阵和反 Hermite 矩阵
- 正交矩阵和酉矩阵
性质://TODO!
形式:A=UΣVH=U(Δr000)VH
求法:
- 根据 ATA 或 AAT 求矩阵的正奇异值
- 计算 ATA 的 n 个标准正交特征向量,一定是正交的,按照特征值λ1,...,λn大小降序排列并标准化为 ϵ1,...,ϵn
- V=(ϵ1,...,ϵn) ,令 V1=(ϵ1,...,ϵk),其中 k 为正特征值对应的特征向量
- U=AV1Δr−1 ,其中 Δr=dialog(λ1,...,λk),即正奇异值
TODO!
- 矩阵的左、右逆
- 矩阵的广义逆(减逆,加逆,最小二乘逆)
定义:左逆满足 AL−A=In ,右逆满足 AAR−=Im
左逆的求法(求右逆可以转置成高阵求左逆再转置):
- 求一个左逆:AL−=(AHA)−1AH 对应的求一个右逆 AR−=AH(AAH)−1
- 求一般左逆:
求法:
满秩分解法:A=BC 则 A+=CH(CCH)−1(BHB)−1BH
特别地,当矩阵为列满秩/��满秩时,退化成左逆/右逆
左逆:AL−=(AHA)−1AH 对应的求一个右逆 AR−=AH(AAH)−1
奇异值分解法:A=UΣVH 则 A+=VΣ−1UH
应用:
最佳最小二乘法:x0=A+b 为 Ax=b 的最佳最小二乘解
A+A 是正交投影,将向量 x 投影到 R(A+) 的空间上;
AA+ 是正交投影,将向量 x 投影到 R(A) 的空间上
A=C(CHC)−1CH
- 向量范数、矩阵范数的计算
- 矩阵函数值的计算
- 一阶线性常微分方程组
向量范数:∣∣x∣∣p=(∑i=1n∣xi∣p)p1
常用的矩阵范数 A=(aij)m∗n:
- 列和范数:最大的列和 ∣∣A∣∣1=max1≤j≤n{∑i=1m∣aij∣}
- 行和范数:最大的行和 ∣∣A∣∣∞=max1≤i≤m{∑j=1n∣aij∣}
- 谱范数:矩阵 AHA 最大特征值开根号 ∣∣A∣∣2=maxλ(AHA)
- Frobenius 范数:所有元素模的平方和开根号 ∣∣A∣∣F=(∑i=1m∑j=1n∣aij∣2)21
- eA=∑k=0∞k!1Ak
- sinA=∑k=0∞(2k+1)!(−1)kA2k+1
- cosA=∑k=0∞(2k)!(−1)kA2k
- ln(I+A)=∑k=1∞k(−1)kAk,ρ(A)<1
- (I−A)−1=∑k=0∞Ak,ρ(A)<1
方法一:Jordan 标准形法
f(A)=P(f(J))P−1
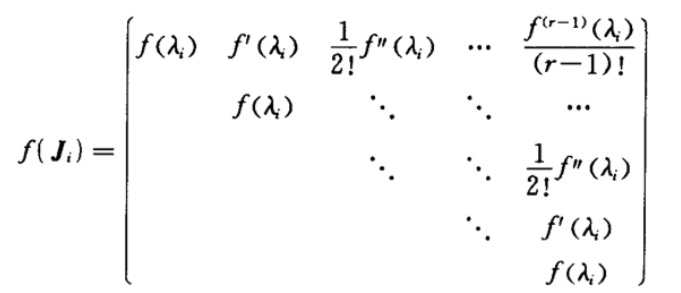
方法二:最小多项式法(待定系数法)
- 求最小多项式 mA(λ)=(λ−λ1)k1...(λ−λs)ks,∑ni=m
- 令 g(λ)=c0+c1λ+...cm−1λm−1
- 根据方程确定系数
⎩⎨⎧g(λi)g′(λi)gni−1(λi)=f(λi)=f′(λi)⋮=fni−1(λi)
- f(A)=g(A)=c0+c1A+...+cm−1Am−1
求解:X′(t)=AX(t)。通解为 eA(t−t0)X(t0);
求解:X′(t)=AX(t)+f(t)。通解为 eA(t−t0)X(t0)+∫t0teA(t−s)f(s)ds
- 求解 K 积和 H 积
- 利用向量化算子和 K 积解矩阵方程
A⊗B=a11Ba21B⋮am1Ba12Ba22B⋮am2B⋯⋯⋱⋯a1nBa2nB⋮amnB
A∘B=a11b11a21b21⋮am1bm1a12b12a22b22⋮am2bm2⋯⋯⋱⋯a1nb1na2nb2n⋮amnbmn
- tr(A⊗B)=tr(A)∗tr(B)
- ∣Am×m⊗Bn×n∣=∣A∣n∣B∣m
- rank(A⊗B)=rank(A)rank(B)
- A⊗B 特征值是 λiuj,特征向量是 (xi⊗yj)
- (A⊗In)+(Im⊗B) 的特征值是 λi+uj,特征向量是 (xi⊗yj)
- A∼JA,B∼JB 则 (A⊗B)∼(JA∼JB)
Vec(ABC)=(CT⊗A)Vec(B)
解矩阵方程:在方程两边运用向量化算子转化成线性方程组求解。
下三角矩阵为消元矩阵(类似方程组的高斯消去法)。
高斯消元过程能够进行到底当且仅当每一步的主元素 aii 都不为 0。




- 高斯消元
当矩阵阶数很高时,消元法相当麻烦。
Crout 分解 => LDU => Doolittle/Cholesky(根号)
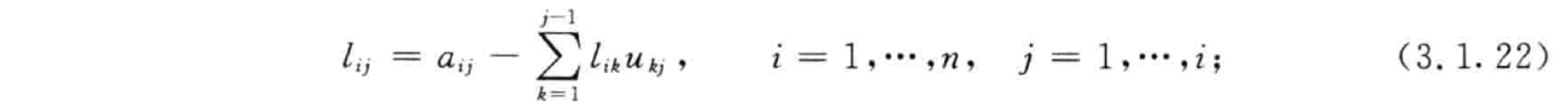
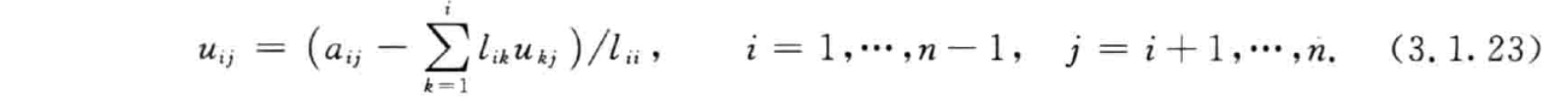


(不常用)斯密特正交法 Q=AB ;则 A=QB−1=QR
(计算工作量较大,在稀疏矩阵有优势)Givens 方法
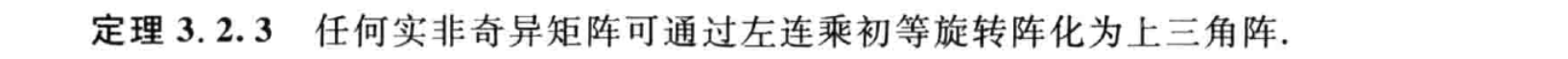
Rij=[c−ssc]
RijA=R A=Rij−1R=RijTR Q=RijT
Housholder 方法
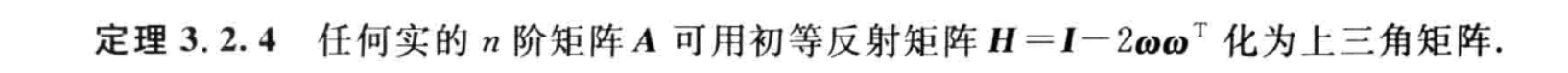
ω(i)=∣αi−∣αi∣ei∣αi−∣αi∣ei
HA=R A=H−1R Q=H−1=HT



将 A 做初等行变换,取 A 的前 r 列作为矩阵 B,取 A 行标准形的前 r 行作为矩阵 C;
或者,将 A 做初等列变换,取 A 列标准形的前 r 列作为矩阵 B,取 A 的前 r 行作为矩阵 C;

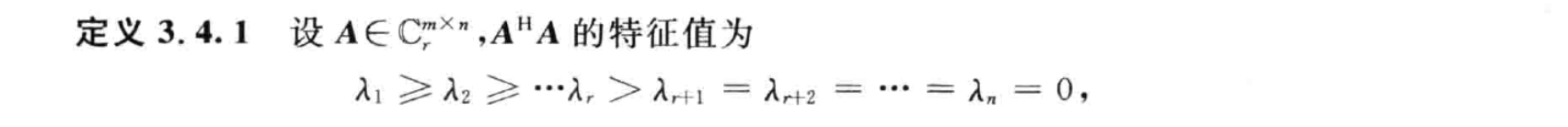


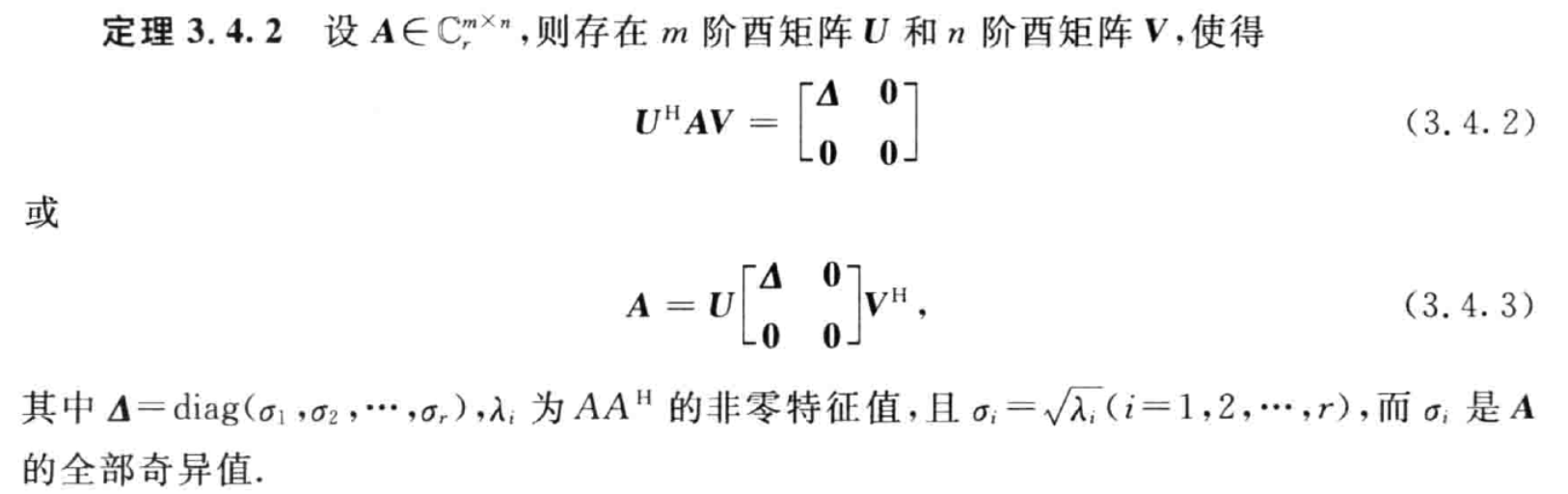
- 求出 A 的奇异值,为 AHA 或 AAH 的正特征值的开根号,利用较小的阶数矩阵求
- 分别求出 AAH ,AHA 对应的归一化特征向量 αi,βj
- 令 U=(α1,...,αm) V=(β1,...,βn)H




可以验证,酉矩阵(推广的正交矩阵)、埃尔米特矩阵(推广的对称矩阵),是正规矩阵。



A=∑λi(∣αi∣1⋅αiαiH)



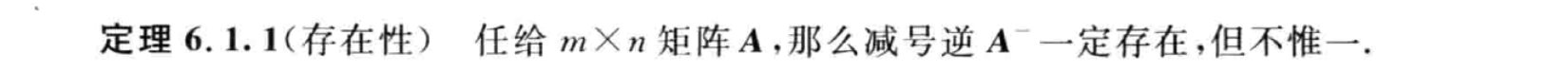
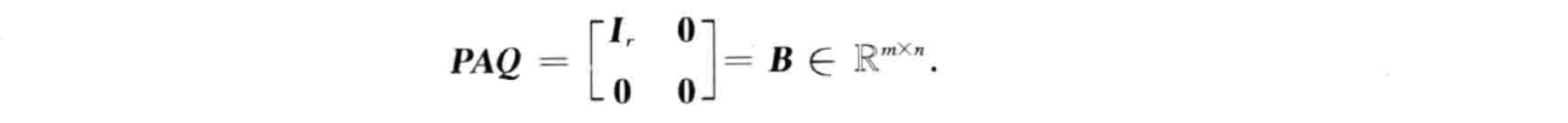
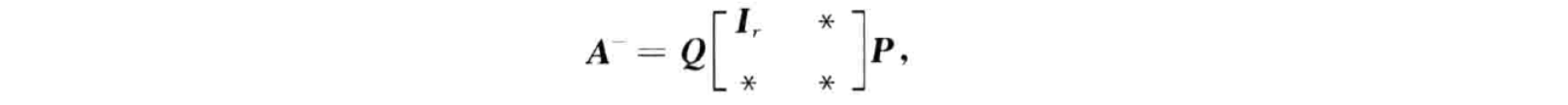






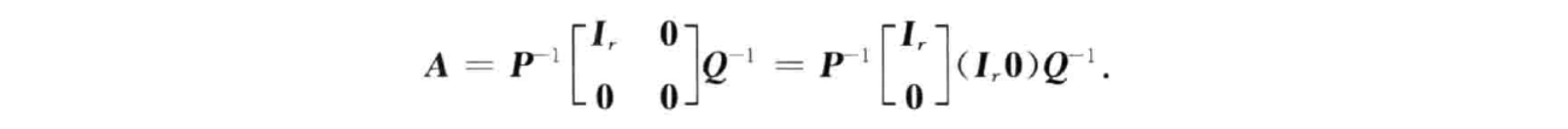
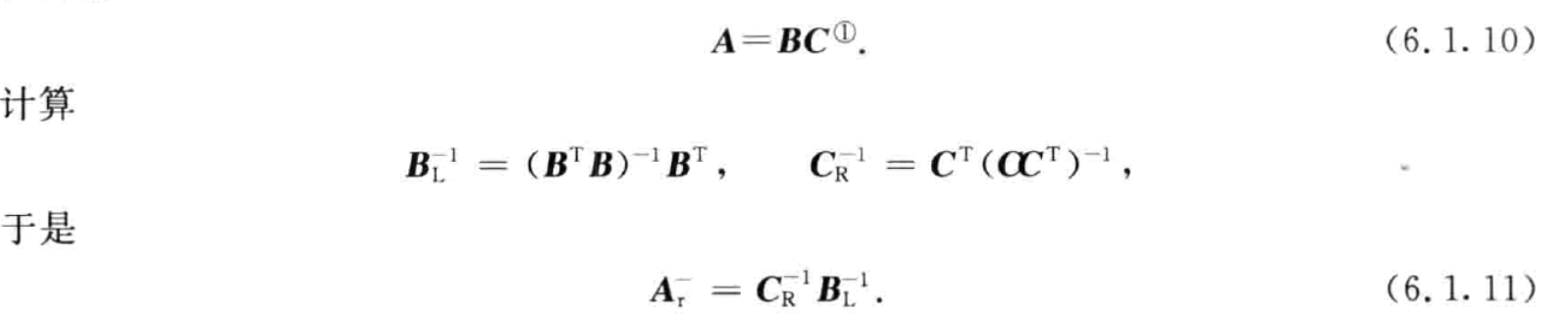
求法:直接是左右逆的等式