本文记录了牛客网剑指offer JZ01-JZ15的刷题过程。

代码均由 cpp 实现。

cpp 知识梳理： 菜鸟教程cpp Vector容器浅析

二维数组的查找（中等）

描述：在一个二维数组中（每个一维数组的长度相同），每一行都按照从左到右递增的顺序排序，每一列都按照从上到下递增的顺序排序。请完成一个函数，输入这样的一个二维数组和一个整数，判断数组中是否含有该整数。

[

[1,2,8,9], [2,4,9,12], [4,7,10,13], [6,8,11,15]

]

题解：采用二分法求解：二分法的应用需要两个方向，因此选取右上角的元素作为中间元素，比这个元素大则往其下方寻找（纵坐标加一），比其小则往左方寻找（横坐标减一），相等则返回 true. 遍历至边界外则返回 false.

复杂度分析：

时间复杂度：O( m+n ) ，m为行数，n为列数

空间复杂度：O( 1 )

代码：

class Solution {
public:
    bool Find(int target, vector<vector<int> > array) {
        int m=array.size();
        int n=array[0].size();
        int i=m-1, j=0;
        while(i>=0 && j>=0 && i<m && j<n){
            if(target==array[i][j]){
                return true;
            }
            else if(target>array[i][j]){
                j++;
            }
            else if(target<array[i][j]){
                i--;
            }
        }
        return false;
    }
};

替换空格

描述：请实现一个函数，将一个字符串中的每个空格替换成“%20”。

题解：设置一个字符数组，遍历字符串，不是空格则赋值，是空格则分别赋值三个字符。遍历完毕加上NUL字符，最后用字符数组转化至字符串。假设题解字符串长度不超过1000。

代码：

class Solution {
public:
    string replaceSpace(string s) {
        char * newString = (char*)malloc(1000);
        int j=0;
        for(int i=0;i<s.length();i++){
            if(s[i]!=' '){
                newString[j++]=s[i];
            }
            else{
                newString[j++]='%';
                newString[j++]='2';
                newString[j++]='0';
            }
        }
        newString[j]='\0';
        string s1(newString);
        return s1;
    }
};

从尾到头打印链表

描述：输入一个链表的头节点，按链表从尾到头的顺序返回每个节点的值（用数组返回）。

题解：

• 解1: 通过std::reverse() 函数 std::reverse(vec.begin(), vec.end())
• 解2: 通过递归求解，先深入至链表尾部，再逐级添加元素。
• 解3: 通过栈的先进后出求解。

代码：

class Solution {
public:
    vector<int> printListFromTailToHead(ListNode* head) {
        stack<int> v1;
        ListNode* p=head;
        while(p!=NULL){
            v1.push(p->val);
            p=p->next;
        }
        vector<int> v2;
        while(!v1.empty()){
            v2.push_back(v1.top());
            v1.pop();
        }
        return v2;
    }
};

重建二叉树

描述：输入某二叉树的前序遍历和中序遍历的结果，请重建出该二叉树。假设输入的前序遍历和中序遍历的结果中都不含重复的数字。例如输入前序遍历序列{1,2,4,7,3,5,6,8}和中序遍历序列{4,7,2,1,5,3,8,6}，则重建二叉树并返回。

题解：用递归求解，先序遍历结果第一个总是根，在中序遍历中查找根的位置，中序遍历序列以左则是左子树子序列，以右则是右子树子序列。从左子树的数量可以从先序序列中得到先序子序列。

代码：

class Solution {
public:
    TreeNode* reConstructBinaryTree(vector<int> pre,vector<int> vin) {
        //若遍历结果为空，则返回NULL
        if(pre.empty())
            return NULL;
        //新建根节点，赋值为先根遍历的第一个元素
        TreeNode * node =(TreeNode *)malloc(sizeof(TreeNode));
        node->val=pre[0];
        //查找根在中序遍历的位置
        int index=0;
        while(index<vin.size() && pre[0]!=vin[index])
            index++;
        //根在中序遍历位置的左方为左子树，右方为右子树
        //可由中序遍历结果左子树的节点个数知道先序遍历序列即根节点后先是左子树的节点，后才是右子树的节点
        vector<int> subLPre(pre.begin()+1,pre.begin()+index+1);
        vector<int> subRPre(pre.begin()+index+1,pre.end());
        vector<int> subLVin(vin.begin(),vin.begin()+index);
        vector<int> subRVin(vin.begin()+index+1,vin.end());
        //获得左子树的两种遍历结果和右子树的两种遍历结果
        //通过递归添加至二叉树中
        node->left=reConstructBinaryTree(subLPre,subLVin);
        node->right=reConstructBinaryTree(subRPre, subRVin);
        //返回根节点
        return node;
    }
};

用两个栈实现队列

描述：用两个栈来实现一个队列，分别完成在队列尾部插入整数(push)和在队列头部删除整数(pop)的功能。 队列中的元素为int类型。保证操作合法，即保证pop操作时队列内已有元素。

题解：第一想法是在第一个栈中实现存放，第二个栈仅仅作为中转将栈逆转过来。讨论中的解是同时应用两个栈实现工作，其中一个栈存放入栈数据，另一个栈存放即将出栈（出队）数据，仅仅在出栈数据栈没有元素时才将第一个存放数据的栈逆转放到第二个栈中。

代码：

class Solution
{
public:

    void push(int node) {
        stack1.push(node);
    }

    int pop() {
        //队列空
        if(stack1.empty()&&stack2.empty());
        //出队栈为空则先将数据栈中内容逆转至出队栈
        if(stack2.empty()){
            while(!stack1.empty()){
                stack2.push(stack1.top());
                stack1.pop();
            }
        }
        //出队
        int val=stack2.top();
        stack2.pop();
        return val;
    }

private:
    stack<int> stack1;
    stack<int> stack2;
};

旋转数组的最小数字

描述：把一个数组最开始的若干个元素搬到数组的末尾，我们称之为数组的旋转。输入一个非递减排序的数组的一个旋转，输出旋转数组的最小元素。NOTE：给出的所有元素都大于0，若数组大小为0，请返回0

题解：采用二分法，考虑中值与右端点进行比较，若比右端点大，则最小值在中值到右端点之间；若比右端点小，则最小值在左端点到中值之间；若相等则需逐步缩进。

代码：

class Solution {
public:
    int minNumberInRotateArray(vector<int> rotateArray) {
    if(rotateArray.empty())return 0;
    int left=0;
    int right=rotateArray.size()-1;
    int mid=(left+right)/2;
    while(left<right-1){
        if(rotateArray[mid]>rotateArray[right]){
        left=mid;
        }
        else if(rotateArray[mid]<rotateArray[right]){
        right=mid;
        }
        else right--;
        mid=(left+right)/2;
    }
    //考虑 left == right-1 的情况
    return rotateArray[left]<rotateArray[right]?rotateArray[left]:rotateArray[right];
    }
};

斐波那契数列

$f(n)=f(n-1)+f(n+1), f(0)=0, f(1)=1$

动态优化代码：

class Solution {
public:
    int Fibonacci(int n) {
        if(n==0)return 0;
        if(n==1)return 1;
        int a=0, b=1, c;
        for(int i=0;i<n-1;i++){
            c = a + b;
            a = b;
            b = c;
        }
        return c;
    }
};

跳台阶

$f(n)=f(n-1)+f(n-2), f(0)=1, f(1)=1$

动态优化代码：

class Solution {
public:
int jumpFloor(int number) {
    int a=1, b=2, c;
    if(number<=2)return number;
    for(int i=0;i<number-2;i++){
        c=a+b;
        a=b;
        b=c;
    }
    return c;
    }
};

跳台阶拓展问题

$f(n)=\sum_{i=0}^{n-1}f(i)=2^{n-1}, f(0)=1, f(1)=1$

动态优化代码：

class Solution {
public:
    int jumpFloorII(int number) {

    /*
    *数学方法直接得出
    */
    return pow(2, number-1);

    if(number<=2)return number;
    vector<int> v(number+1,0);
    v[0]=0;
    v[1]=1;
    v[2]=2;
    for(int i=3;i<=number;i++){
        for(int j=0;j<i;j++){
            v[i]+=v[j];
        }
        v[i]++;
    }
    return v[number];
    }
};

矩形覆盖

$f(n)=f(n-1)+f(n-2),f(1)=1,f(2)=2$

描述：我们可以用21的小矩形横着或者竖着去覆盖更大的矩形。请问用n个21的小矩形无重叠地覆盖一个2*n的大矩形，从同一个方向看总共有多少种不同的方法？

题解：即可以用前几题的动态规划解题，也可以看做是 1 和 2 的元素排列其中总数为 n，那么对于正整数 n, 从没有一个 2 到有 $\lfloor n/2 \rfloor$ 个 2, 总数从 n 到 $n-\lfloor n/2 \rfloor$个，故共有 $\sum_{i=0}^{\lfloor n/2 \rfloor}C^{i}_{n-i}$种

代码：

class Solution {
public:
    int rectCover(int number) {
        if(number==0)return 0;
        /*
        * C(n,0)+C(n-1,1)+C(n-2,2)+...+C(n/2,n/2)
        */
        int n = number/2;
        int ret=1;
        for(int i=1;i<=n;i++){
            int temp=1;
            for(int j=1;j<=i;j++){
                temp*=number-j-i+1;
                temp/=j;
            }
            ret+=temp;
        }
        return ret;
    }
};

二进制中1的个数

描述：

输入一个整数，输出该数32位二进制表示中1的个数。其中负数用补码表示。

题解：

有一种巧妙的方法可以消去最右边的 1 ，即 n = n & (n-1)

代码：

class Solution {
public:
    int  NumberOf1(int n) {
        int cnt=0;
        while(n!=0){
            cnt++;
            n = n & (n-1);
        }
        return cnt;
    }
};

数值的整数次方

描述：

给定一个double类型的浮点数base和int类型的整数exponent。求base的exponent次方。保证base和exponent不同时为0。不得使用库函数，同时不需要考虑大数问题，也不用考虑小数点后面0的位数。

题解：

采用快速迭代算法，例如

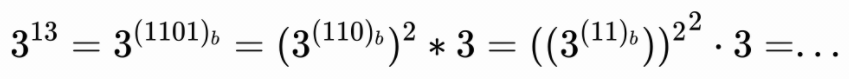
代码：

class Solution {
    public:
    double Power(double base, int exponent) {
        double ans = 1;
        if( base==0 && exponent==0 );//
        if(exponent<0){
            base = 1/base;
            exponent = -exponent;
        }
        double temp = base;
        while(exponent>0){
            ans*=((exponent&1)?temp:1);
            exponent>>=1;
            temp=temp*temp;
        }
        return ans;
    }
};

调整数组顺序使奇数位于偶数之前

描述：

输入一个整数数组，实现一个函数来调整该数组中数字的顺序，使得所有的奇数位于数组的前半部分，所有的偶数位于数组的后半部分，并保证奇数和奇数，偶数和偶数之间的相对位置不变。

题解：

采用从两边扫描，左边扫描奇数从左往右添加，右边扫描偶数从右往左添加，直到数组元素重合。

代码：

class Solution {
    public:
    vector<int> reOrderArray(vector<int>& array) {
        vector<int> v(array.size());
        int left=0, right=array.size()-1;
        for(int i=left,j=right;left<=right;i++,j--){
            if(array[i]%2)v[left++]=array[i];
            if(!(array[j]%2))v[right--]=array[j];
        }
        return v;
    }
};

链表倒数最后k个结点

描述：

输入一个链表，输出一个链表，该输出链表包含原链表中从倒数第k个结点至尾节点的全部节点。

如果该链表长度小于k，请返回一个长度为 0 的链表。

题解：

• 采用双指针：指针 p 先走 k 步，若没走到就到尾则返回 NULL; 然后指针 q 和 p 一起走直到 p 到链尾，返回 q
• 用栈
• 递归

代码：

class Solution {
    public:
    ListNode* FindKthToTail(ListNode* pHead, int k) {
        ListNode *p=pHead;
        int len=0;
        while(len<k){
            len++;
            if(p==NULL){
                return NULL;
            }
            p=p->next;
        }
        ListNode *q=pHead;
        while(p){
            p=p->next;
            q=q->next;
        }
        return q;
    }
};

反转链表

描述：输入一个链表，反转链表后，输出新链表的表头

题解：

用两个指针遍历逆转指向，注意判空和中间结点的保存。

代码：

class Solution {
    public:
    ListNode* ReverseList(ListNode* pHead) {
        ListNode* p1=pHead, *p2;
        if(p1==NULL||p1->next==NULL)return p1;
        p2=p1->next;
        p1->next=NULL;
        while(p2){
            ListNode* temp=p2->next;
            p2->next = p1;
            p1 = p2;
            p2 = temp;
        }
        return p1;
    }
};